おはようございます。管理人のハル(@haru_reha)です。
今回は「平均値」の話です。
おそらく統計量のなかで最も身近で、誰もが知っているものだと思います。
しかし、その性質については曖昧な方も多いのではないでしょうか。
平均値から何が分かるのか、簡単に説明してみます。
平均値とは?
まず、平均値の計算方法です。
これは「データを全て足して、それをデータ数で割る」ですよね。
例えば、30人の患者さんの在院日数を調べたとします。
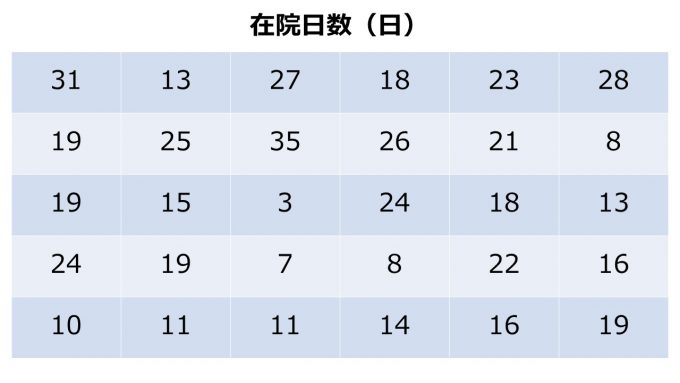
すると平均値は
[31+13+27+18+‥‥+16+19] ÷ 30 = 18.133日
となります。
また別の方法として度数分布表から近似値を計算する方法もあります。
度数分布表は⇓のような表のことで、ここから [ 階級値×相対度数 ] の合計を計算することで平均値の近似値を出すことができます。

つまり
(3 × 0.033) + (8 × 0.133) + (13 × 0.200) +‥‥+(33 × 0.067) = 18.18
となります(先ほどの平均値の計算とほぼ一致)。
他にも「相乗平均」「二乗平均」など、平均値の求め方は色々とあるのですが、これは少し置いておきます。
平均値は何を表すのか?
平均値などの統計量は「データの特徴を1つの数字で表す」役割をもっています。
つまり「データにはバラつきがあり、色々な値をとるが、その中から全データを代表する数値として選びだしたもの」だという捉え方をする必要があります。
統計量には平均値のほかに中央値とか、最頻値、分散、標準偏差などがありますが、それぞれどんな特徴を表すのかは異なります。
平均値の場合は「データのつり合いが取れる点」を表しています。
これはヒストグラムを見るとイメージがつきやすいです。
先ほどの在院日数のデータをヒストグラムで見ると⇓のようになります。

平均値は18.18でしたので、ヒストグラムでいうと⇓の位置になります。

ヒストグラムを「やじろべえ」とみなすと、平均値はそれのつり合いの支点となるように位置します。
平均値の性質
平均値は「データのつり合いがとれる点」だということから、以下のような性質をもっています。
① データは平均値の周辺に分布している
② 多く現れるデータの平均値への影響力は大きい
③ ヒストグラムが左右対称である場合、その対称軸の通る点が平均値になる
(引用)完全独習 統計学入門(ダイヤモンド社)p30
①については、データがおおまかにどの辺りに分布しているのかが分かります。先ほどの在院日数のデータでいえば、平均在院日数は18.1日なので、その辺りで退院する人が多く、少なくとも50日とか100日とかの人はいない(いたとしても少数)だろう、ということを知ることができます。
②については、ヒストグラムで度数が高くなっている値ほど平均値に影響を強く与えているということですね。基本的には正規分布しているデータであれば、最頻値の近くに平均値も位置するはずです。
③については、グラフが左右対称である場合には、ちょうどその真ん中に平均値が位置することを表します。完全な正規分布であれば、平均値・中央値・最頻値が一致しますし、すべての度数が同じデータであっても、平均値はちょうど真ん中にくるはずですよね。
逆に、データのバラつきが大きく、また分布もバラバラの場合ですと、平均値はあまり良い指標とはならないことも分かりますね。
例えば次のようなヒストグラムでは、平均値は赤い矢印の所になりますが、これではデータの特徴をうまく説明できません(平均値付近のデータが少なく、平均値より離れたところに最頻値がある)。

つまり、平均値はバラつきが大きいデータや、分布がバラバラのデータでは代表値として扱いにくいということになります。そのようなときには、基本的には中央値が代表値として採用されます。
まとめ
以上、平均値の性質についてまとめてみました。
研究に慣れないうちは、何かと代表値を平均値にしてしまいがちですが、平均値を代表値とするときには分布を合わせて見ておきたいところですね。
平均値の性質をよく理解しておくことで、自分の研究でデータ解析をする時、論文を読む時などの解釈も変わってくるのではないかと思います。
今回も下記の書籍を参考にさせて頂きましたのでご紹介しておきます。
また、過去の記事で関連するものを挙げておきますので興味のある方はぜひ覗いてみてくださいね。
では、また~。








コメント